CONJUNTOS

DEFINICIÓN DE CONJUNTOS

Un conjunto se determina por extensión cuando se nombran todos sus elementos, y por comprensión cuando se da la característica común de sus elementos.

Los conjuntos también se pueden definir por comprensión utilizando la notación simbólica:

A = {x | x   N, 4 < x < 11}

Se lee: A es un conjunto formado por todos los elementos x tal que x es un número natural mayor que 4 y menor que 11.

DEFINICION

---

La palabra conjunto generalmente la asociamos con la idea de agrupar objetos, por ejemplo un conjunto de discos, de libros, de plantas de cultivo y en otras ocasiones en palabras como hato, rebaño, piara, parcelas, campesinado, familia, etc., es decir la palabra conjunto denota una colección de elementos claramente entre sí, que guardan alguna característica en común. Ya sean números, personas, figuras, ideas y conceptos.

En matemáticas el concepto de conjunto es considerado primitivo y ni se da una definición de este, sino que se trabaja con la notación de colección y agrupamiento de objetos, lo mismo puede decirse que se consideren primitivas las ideas de elemento y pertenencia.

La característica esencial de un conjunto es la de estar bien definido, es decir que dado un objeto particular, determinar si este pertenece o no al conjunto. Por ejemplo si se considera el conjunto de los números dígitos, sabemos que el 3 pertenece al conjunto, pero el 19 no. Por otro lado el conjunto de las bellas obras musicales no es un conjunto bien definido, puesto que diferentes personas puedan incluir distintas obras en el conjunto.

Los objetos que forman un conjunto son llamados miembros o elementos. Por ejemplo el conjunto de las letras de alfabeto; a, b, c, ..., x, y, z. que se puede escribir así:

{ a, b, c, ..., x, y, z}

Como se muestra el conjunto se escribe entre llaves ({}) , o separados por comas (,).

El detallar a todos los elementos de un conjunto entre las llaves, se denomina forma tabular, extensión o enumeración de los elementos.

 Dos conjuntos son iguales si tienen los mismos elementos, por ejemplo:

El conjunto { a, b, c } también puede escribirse:

{ a, c, b }, { b, a, c }, { b, c, a }, { c, a, b }, { c, b, a }

 En teoría de conjuntos se acostumbra no repetir a los elementos por ejemplo:

El conjunto { b, b, b, d, d } simplemente será { b, d }.

---

MEMBRESIA

Los conjuntos se denotan por letras mayúsculas : A, B, C,... por ejemplo:

A={ a, c, b }

B={ primavera, verano, otoño, invierno }

El símbolo Î indicará que un elemento pertenece o es miembro de un conjunto. Por el contrario para indicar que un elemento no pertenece al conjunto de referencia, bastará cancelarlo con una raya inclinada / quedando el símbolo como Ï .

 Ejemplo:

Sea B={ a, e, i, o, u }, a Î B y c Ï B

---

SUBCONJUNTO

Sean los conjuntos A={ 0, 1, 2, 3, 5, 8 } y B={ 1, 2, 5 }

En este caso decimos que B esta contenido en A, o que B es subconjunto de A. En general si A y B son dos conjuntos cualesquiera, decimos que B es un subconjunto de A si todo elemento de B lo es de A también.

Por lo tanto si B es un subconjunto de A se escribe B Ì A. Si B no es subconjunto de A se indicará con una diagonal Ë .

Note que Î se utiliza solo para elementos de un conjunto y Ì solo para conjuntos.

---

UNIVERSO O CONJUNTO UNIVERSAL

El conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal, este conjunto depende del problema que se estudia, se denota con la letra U y algunas veces con la letra S (espacio muestral).

Por ejemplo si solo queremos referirnos a los 5 primeros números naturales el conjunto queda:

U={ 1, 2, 3, 4, 5 }

Forma alternativa para indicar conjuntos de gran importancia:

• Conjunto de números naturales (enteros mayores que cero) representados por la letra N donde

N={ 1, 2, 3, .... }

• Conjunto de números enteros positivos y negativos representados por la letra Z donde

Z={..., -2, -1, 0, 1, 2, ... }

• Conjunto de números racionales (números que se representan como el cociente de dos números enteros {fracciones }). Estos números se representan por una Q
• Conjunto de números irracionales (números que no puedan representarse como el cociente de dos números enteros) representados por la letra I.
• Conjunto de los números reales que son los números racionales e irracionales es decir todos, representados por R.

Todos estos conjuntos tienen un número infinito de elementos, la forma de simbolizarlos por extensión o por enumeración es de gran utilidad cuando los conjuntos a los que se hace referencia tienen pocos elementos para poder trabajar con ellos se emplean la notación llamada comprehensión.

Por ejemplo, la denotar el conjunto de los números naturales menores que 60. Aquí U es el conjunto N y se tiene una propiedad que caracteriza a los elementos del conjunto: ser menores que 60.

Para indicar esta situación empleamos la simbología del álgebra de conjuntos:

{ x/x Î N ; x<60 }

En esta expresión se maneja un conjunto de x que pertenece a los números naturales (N) y además que los valores de x son menores que 60.

Ahora si se desea trabajar con conjuntos que manejen intervalos estos pueden ser representados por medio de una expresión algebraica; supongamos que se desea expresar los números enteros (Z) entre -20 y 30 el conjunto quedaría de la manera siguiente:

{ x/x Î Z ; -20 £ x £ 30 }

También se puede expresar el valor de un conjunto indicando la pertenencia o no pertenencia a uno diferente, por ejemplo

L={ 1, 3, 4, 6, 9 }

P={ x/x Î N ; X Ï L }

En el conjunto P se indica que los elementos x de un conjunto pertenecen a los números naturales y además x no pertenece al conjunto L.

---

OPERACIONES CON CONJUNTOS

---

UNION

La unión de dos conjuntos A y B la denotaremos por A È B y es el conjunto formado por los elementos que pertenecen al menos a uno de ellos ó a los dos. Lo que se denota por:

A È B = { x/x Î A ó x Î B }

Ejemplo: Sean los conjuntos A={ 1, 3, 5, 7, 9 } y B={ 10, 11, 12 }

A È B ={ 1, 3, 5, 7, 9, 10, 11, 12 }

---

INTERSECCION

Sean A={ 1, 2, 3, 4, 5, 6, 8, 9 } y B={ 2, 4, 8, 12 }

Los elementos comunes a los dos conjuntos son: { 2, 4, 8 }. A este conjunto se le llama intersección de A y B; y se denota por A Ç B, algebraicamente se escribe así:

A Ç B = { x/x Î A y x Î B }

Y se lee el conjunto de elementos x que están en A y están en B.

Ejemplo:

Sean Q={ a, n, p, y, q, s, r, o, b, k } y P={ l, u, a, o, s, r, b, v, y, z }

Q Ç P={ a, b, o, r, s, y }

---

CONJUNTO VACIO

Un conjunto que no tiene elementos es llamado conjunto vacío ó conjunto nulo lo que denotamos por el símbolo Æ .

Por ejemplo:

Sean A={ 2, 4, 6 } y B={ 1, 3, 5, 7 } encontrar A Ç B.

A Ç B= { }

El resultado de A Ç B= { } muestra que no hay elementos entre las llaves, si este es el caso se le llamará conjunto vacío ó nulo y se puede representar como:

A Ç B=Æ

---

CONJUNTOS AJENOS

Sí la intersección de dos conjuntos es igual al conjunto vacío, entonces a estos conjuntos les llamaremos conjuntos ajenos, es decir:

Si A Ç B = Æ entonces A y B son ajenos.

---

COMPLEMENTO

El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A y se denota como A' y que se representa por comprehensión como:

A'={ x Î U/x y x Ï A }

Ejemplo:

Sea U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }

A= { 1, 3, 5, 7, 9 } donde A Ì U

El complemento de A estará dado por:

A'= { 2, 4, 6, 8 }

---

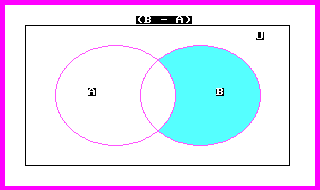
DIFERENCIA

Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprehensión como:

A - B={ x/x Î A ; X Ï B }

Ejemplo:

Sea A= { a, b, c, d } y

B= { a, b, c, g, h, i }

A - B= { d }

En el ejemplo anterior se observa que solo interesan los elementos del conjunto A que no estén en B. Si la operación fuera B - A el resultado es

B – A = { g, h, i }

E indica los elementos que están en B y no en A.

---

DIAGRAMAS DE VENN

Los diagramas de Venn que de deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.

La manera de representar el conjunto Universal es un rectángulo, ó bien la hoja de papel con que se trabaje.

Un ejemplo de la representación del conjunto universal se muestra como:

Los conjuntos se representan por medio de dibujos dentro del rectángulo, los aspectos de interés se resaltan sombreando las áreas respectivas. En el caso de este curso las indicaremos por medio de un color azul por ejemplo:

bibliografía:

http://colposfesz.galeon.com/est501/conjunto/teoconj.htm

Integrantes:
Seyra Guanilo
Rocio Gonzáles
Fiorella Marines
Yurits Rosas
Mariely Sanchez
Kiara Silva